Liars, cheats, scammers and the Schnorr signature

How sure are you that the cryptography underlying Bitcoin is secure? With regard to one future development of Bitcoin's crypto, in discussions in public fora, I have more than once confidently asserted "well, but the Schnorr signature has a security reduction to ECDLP". Three comments on that before we begin:

• If you don't know what "reduction" means here, fear not, we will get deeply into this here.
• Apart from simply hearing this and repeating it, I was mostly basing this on a loose understanding that "it's kinda related to the soundness proof of a sigma protocol" which I discussed in my ZK2Bulletproofs paper, which is true - but there's a lot more involved.
• The assertion is true, but there are caveats, as we will see. And Schnorr is different from ECDSA in this regard, as we'll also see, at the end.

But why write this out in detail? It actually came sort of out of left field. Ruben Somsen was asking on slack about some aspect of Monero, I forget, but it prompted me to take another look at those and other ring signatures, and I realised that attempting to understand the security of those more complex constructions is a non-starter unless you really understand why we can say "Schnorr is secure" in the first place.

Liars and cheats

The world of "security proofs" in cryptography appears to be a set of complex stories about liars - basically made up magic beans algorithms that pretend to solve things that nobody actually knows how to solve, or someone placing you in a room and resetting your clock periodically and pretending today is yesterday - and cheats, like "let's pretend the output of the hash function is
\(x\), because it suits my agenda for it to be \(x\)" (at least in this case the lying is consistent - the liar doesn't change his mind about \(x\); that's something!).

I hope that sounds crazy, it mostly really is :)

(Concepts I am alluding to include: the random oracle, a ZKP simulator, extractor/"forking", an "adversary" etc. etc.)

Preamble: the reluctant Satoshi scammer

The material of this blog post is pretty abstract, so I decided to spice it up by framing it as some kind of sci-fi 😄

Imagine you have a mysterious small black cube which you were given by an alien that has two slots you can plug into to feed it input data and another to get output data, but you absolutely can't open it (so like an Apple device, but more interoperable), and it does one thing only, but that thing is astonishing: if you feed it a message and a public key in its input slot, then it'll sometimes spit out a valid Schnorr signature on that message.

Well in 2019 this is basically useless, but after considerable campaigning (mainly by you, for some reason!), Schnorr is included into Bitcoin in late 2020. Delighted, you start trying to steal money but it proves to be annoying.

First, you have to know the public key, so the address must be reused or something similar. Secondly (and this isn't a problem, but is weird and will become relevant later): the second input slot is needed to pass the values of the hash function sha2 (or whatever is the right one for our signature scheme) into the black box for any data it needs to hash. Next problem: it turns out that the device only works if you feed it a few other signatures of other messages on the same public key, first. Generally speaking, you don't have that. Lastly, it doesn't always work for any message you feed into it (you want to feed in 'messages' which are transactions paying you money), only sometimes.

With all these caveats and limitations, you fail to steal any money at all, dammit!

Is there anything else we can try? How about we pretend to be someone else? Like Satoshi? Hmm ...

For argument's sake, we'll assume that people use the Schnorr Identity Protocol (henceforth SIDP), which can be thought of as "Schnorr signature without the message, but with an interactive challenge". We'll get into the technicals below, for now note that a signature doesn't prove anything about identity (because it can be passed around), you need an interactive challenge, a bit like saying "yes, give me a signature, but I choose what you sign".

So to get people to believe I'm Satoshi (and thus scam them into investing in me perhaps? Hmm sounds familiar ...) I'm going to somehow use this black box thing to successfully complete a run of SIDP. But as noted it's unreliable; I'll need a bunch of previous signatures (let's pretend that I get that somehow), but I also know this thing doesn't work reliably for every message, so the best I can do is probably to try to scam 1000 people simultaneously. That way they might reasonably believe that their successful run represents proof; after all it's supposed to be impossible to create this kind of proof without having the private key - that's the entire idea of it! (the fact that it failed for other people could be just a rumour, after all!)

So it's all a bit contrived, but weirder scams have paid off - and they didn't even use literally alien technology!

So, we'll need to read the input to our hash function slot from the magic box; it's always of the form:

message || R-value

... details to follow, but basically \(R\) is the starting value in the SIDP, so we pass it to our skeptical challenger(s). They respond with \(e\), intended to be completely random to make our job of proving ID as hard as possible, then we trick our black box - we don't return SHA2(\(m||R\)) but instead we return \(e\). More on this later, see "random oracle model" in the below. Our magic box outputs, if successful, \(R, s\) where \(s\) is a new random-looking value. The challenger will be amazed to see that:

\(sG = R + eP\)

is true!! And the millions roll in.

If you didn't get in detail how that scam operated, don't worry, we're going to unpack it, since it's the heart of our technical story below. The crazy fact is that our belief that signatures like the Schnorr signature (and ECDSA is a cousin of it) is mostly reliant on basically the argument above.

But 'mostly' is an important word there: what we actually do, to make the argument that it's secure, is stack that argument on top of at least 2 other arguments of a similar nature (using one algorithm as a kind of 'magic black box' and feeding it as input to a different algorithm) and to relate the digital signature's security to the security of something else which ... we think is secure, but don't have absolute proof.

Yeah, really.

We'll see that our silly sci-fi story has some practical reality to it - it really is true that to impersonate is a bit more practically feasible than to extract private keys, and we can even quantify this statement, somewhat.

But not the magic cube part. That part was not real at all, sorry.

Schnorr ID Protocol and signature overview

I have explained SIDP with reference to core concepts of Sigma Protocols and Zero Knowledge Proofs of Knowledge in Section 3.2 here . A more thorough explanation can be found in lots of places, e.g. Section 19.1 of Boneh and Shoup. Reviewing the basic idea, cribbing from my own doc:

Prover \(\mathbb{P}\) starts with a public key \(P\) and a corresponding private key \(x\) s.t. \(P = xG\).

\(\mathbb{P}\) wishes to prove in zero knowledge, to verifier \(\mathbb{V}\), that he knows \(x\).

\(\mathbb{P}\) → \(\mathbb{V}\) : \(R\) (a new random curve point, but \(\mathbb{P}\) knows \(k\) s.t. \(R = kG\) )

\(\mathbb{V}\) → \(\mathbb{P}\): \(e\) (a random scalar)

\(\mathbb{P}\) → \(\mathbb{V}\): \(s\)(which \(\mathbb{P}\) calculated from the equation \(s = k + ex\))

Note: the transcript of the conversation would here be: \((R, e, s)\).

Verification works fairly trivially: verifier checks \(sG \stackrel{?}{=} R + eP\). See previously mentioned doc for details on why this is supposedly zero knowledge, that is to say, the verifier doesn't learn anything about the private key from the procedure.

As to why it's sound - why does it really prove that the Prover knows \(x\), see the same doc, but in brief: if we can convince the prover to re-run the third step with a modified second step (but the same first step!), then he'll be producing a second signature \(s'\) on a second random \(e'\), but with the same \(k\) and \(R\) , thus:

\(x = \frac{s' - s}{e' -e}\)

So we say it's "sound" in the specific sense that only a knower-of-the-secret-key can complete the protocol. But more on this shortly!

What about the famous "Schnorr signature"? It's just an noninteractive version of the above. There is btw a brief summary in this earlier blog post, also. Basically replace \(e\) with a hash (we'll call our hash function \(\mathbb{H}\)) of the commitment value and the message we want to sign \(m\):

\(e = \mathbb{H}(m||R)\)

; as mentioned in the just-linked blog post, it's also possible to add other stuff to the hash, but these two elements at least are necessary to make a sound signature.

As was noted in the 80s by Fiat and Shamir, this transformation is generic to any zero-knowledge identification protocol of the "three pass" or sigma protocol type - just use a hash function to replace the challenge with H(message, commitment) to create the new signature scheme.

Now, if we want to discuss security, we first have to decide what that even means, for a signature scheme. Since we're coming at things from a Bitcoin angle, we're naturally focused on preventing two things: forgery and key disclosure. But really it's the same for any usage of signatures. Theorists class security into at least three types (usually more, these are the most elementary classifications):

• Total break
• Universal forgery
• Existential forgery

(Interesting historical note: this taxonomy is due to Goldwasser, Micali and Rackoff - the same authors who introduced the revolutionary notion of a "Zero Knowledge Proof" in the 1980s.)

Total break means key disclosure. To give a silly example: if \(k=0\) in the above, then \(s = ex\) and, on receipt of \(s\), the verifier could simply multiply it by the modular inverse of \(e\) to extract the private key . A properly random \(k\) value, or 'nonce', as explained ad nauseam elsewhere, is critical to the security. Since this is the worst possible security failure, being secure against it is considered the weakest notion of "security" (note this kind of "reverse" reasoning, it is very common and important in this field).

The next weakest notion of security would be security against universal forgery - the forger should not be able to generate a signature on any message they are given. We won't mention this too much; we will focus on the next, stronger notion of "security":

"Security against existential forgery under adaptive chosen message attack", often shortened to EUF-CMA for sanity (the 'adaptive(ly)' sometimes seems to be dropped, i.e. understood), is clearly the strongest notion out of these three, and papers on this topic generally focus on proving this. "Chosen message" here refers to the idea that the attacker even gets to choose what message he will generate a verifying forgery for; with the trivial restriction that it can't be a message that the genuine signer has already signed.

(A minor point: you can also make this definition more precise with SUF-CMA (S = "strongly"), where you insist that the finally produced signature by the attacker is not on the same message as one of the pre-existing signatures. The famous problem of signature malleability experienced in ECDSA/Bitcoin relates to this, as noted by Matt Green here.)

I believe there are even stronger notions (e.g. involving active attacks) but I haven't studied this.

In the next, main section of this post, I want to outline how cryptographers try to argue that both the SIDP and the Schnorr signature are secure (in the latter case, with that strongest notion of security).

Why the Schnorr signature is secure

Why the SIDP is secure

Here, almost by definition, we can see that only the notion of "total break" makes sense: there is no message, just an assertion of key ownership. In the context of SIDP this is sometimes called the "impersonation attack" for obvious reasons - see our reluctant scammer.

The justification of this is somehow elegantly and intriguingly short:

The SIDP is secure against impersonation = The SIDP is sound as a ZKPOK.

You can see that these are just two ways of saying the same thing. But what's the justification that either of them are true? Intuitively the soundness proof tries to isolate the Prover as a machine/algorithm and screw around with its sequencing, in an attempt to force it to spit out the secret that we believe it possesses. If we hypothesise an adversary \(\mathbb{A}\) who doesn't possess the private key to begin with, or more specifically, one that can pass the test of knowing the key for any public key we choose, we can argue that there's only one circumstance in which that's possible: if \(\mathbb{A}\) can solve the general Elliptic Curve Discrete Logarithm Problem(ECDLP) on our curve. That's intuitively very plausible, but can we prove it?

Reduction

(One of a billion variants on the web, taken from here :))

A mathematician and a physicist were asked the following question:

"Suppose you walked by a burning house and saw a hydrant and a hose not connected to the hydrant. What would you do?"

P: I would attach the hose to the hydrant, turn on the water, and put out the fire.

M: I would attach the hose to the hydrant, turn on the water, and put out the fire.

Then they were asked this question:

"Suppose you walked by a house and saw a hose connected to a hydrant. What would you do?"

P: I would keep walking, as there is no problem to solve.

M: I would disconnect the hose from the hydrant and set the house on fire, reducing the problem to a previously solved form.

The general paradigm here is:

A protocol X is "reducible to" a hardness assumption Y if a hypothetical adversary \(\mathbb{A}\) who can break X can also violate Y.

In the concrete case of X = SIDP and Y = ECDLP we have nothing to do, since we've already done it. SIDP is intrinsically a test that's relying on ECDLP; if you can successfully impersonate (i.e. break SIDP) on any given public key
then an "Extractor" which we will now call a wrapper, acting to control the environment of \(\mathbb{A}\) and running two executions of the second half of the transcript, as already described above, will be able to extract the private key/discrete log corresponding to \(P\). So we can think of that Extractor itself as a machine/algorithm which spits out the \(x\) after being fed in the \(P\), in the simple case where our hypothetical adversary \(\mathbb{A}\) is 100% reliable. In this specific sense:

SIDP is reducible to ECDLP

However, in the real world of cryptographic research, such an analysis is woefully inadequate; because to begin with ECDLP being "hard" is a computational statement: if the group of points on the curve is only of order 101, it is totally useless since it's easy to compute all discrete logs by brute force. So, if ECDLP is "hard" on a group of size \(2\\^k\), let's say, its hardness is measured as the probability of successfully cracking by guessing, i.e. one in two to the \(-k\), (here deliberately avoiding the real measure based on smarter than pure guesses, because it's detail that doesn't affect the rest). Suppose \(\mathbb{A}\) has a probability of success \(\epsilon\); what probability of success does that imply in solving ECDLP, in our "wrapper" model? Is it \(\epsilon\)?

No; remember the wrapper had to actually extract two successful impersonations in the form of valid responses \(s\) to challenge values \(e\). We can say that the wrapper forks \(\mathbb{A}\):

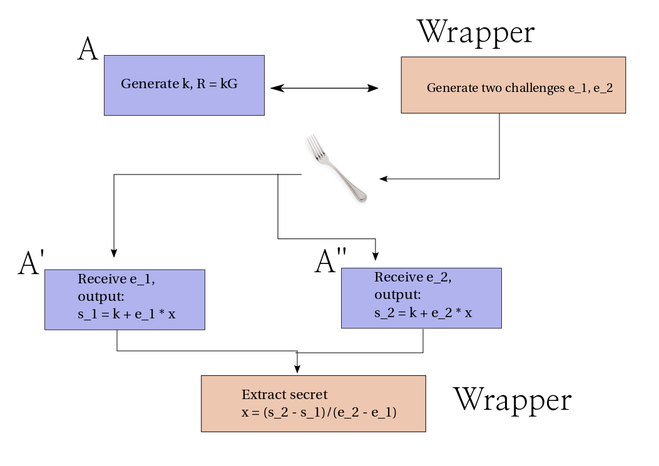
Crudely, the success probability is \(\epsilon^2\); both of those impersonations have to be successful, so we multiply the probabilities. (More exact: by a subtle argument we can see that the size of the challenge space being reduced by 1 for the second run of the protocol implies that the probability of success in that second run is reduced, and the correct formula is \(\epsilon^2 - \frac{\epsilon}{n}\), where \(n\) is the size of the hash function output space; obviously this doesn't matter too much).

How does this factor into a real world decision? We have to go back to the aforementioned "reverse thinking". The reasoning is something like:

• We believe ECDLP is hard for our group, let's say we think you can't do better than p = \(p\) (I'll ignore running time and just use probability of success as a measure, for simplicity).
• The above reduction implies that if we can break SIDP with prob \(\epsilon\)
  , we can also break ECDLP with prob \(\simeq \epsilon^2\).
• This reduction is thus not tight - if it's really the case that "the way to break SIDP is only to break ECDLP" then a certain hardness \(p\) only implies a hardness \(\sqrt{p}\) for SIDP, which we may not consider sufficiently improbable (remember that if \(p = 2^{-128}\), it means halving the number of bits: \(\sqrt{p} = 2^{-64}\)). See here for a nice summary on "non-tight reductions".
• And that implies that if I want 128 bit security for my SIDP, I need to use 256 bits for my ECDLP (so my EC group, say). This is all handwavy but you get the pattern: these arguments are central to deciding what security parameter is used for the underlying hardness problem (here ECDLP) when it's applied in practice to a specific protocol (here SIDP).

I started this subsection on "reductions" with a lame math joke; but I hope you can see how delicate this all is ... we start with something we believe to be hard, but then "solve" it with a purely hypothetical other thing (here \(\mathbb{A}\)), and from this we imply a two-way connection (I don't say equivalence; it's not quite that) that we use to make concrete decisions about security. Koblitz (he of the 'k' in secp256k1) had some interesting thoughts about 'reductionist' security arguments in Section 2.2 and elsewhere in this paper. More from that later.

So we have sketched out how to think about "proving our particular SIDP instance is/isn't secure based on the intractability of ECDLP in the underlying group"; but that's only 2 stacks in our jenga tower; we need MOAR!

From SIDP to Schnorr signature

So putting together a couple of ideas from previous sections, I hope it makes sense to you now that we want to prove that:

"the (EC) Schnorr signature has existential unforgeability against chosen message attack (EUFCMA) if the Schnorr Identity Protocol is secure against impersonation attacks."

with the understanding that, if we succeed in doing so, we have proven also:

"the (EC) Schnorr signature has existential unforgeability against chosen message attack (EUFCMA) if the Elliptic Curve discrete logarithm problem is hard in our chosen EC group."

with the substantial caveat, as per the previous section, that the reduction involved in making this statement is not tight.

(there is another caveat though - see the next subsection, The Random Oracle Model).

This second (third?) phase is much less obvious and indeed it can be approached in more than one way. Boneh-Shoup deals with it in a lot more detail; I'll use this as an outline but dumb it down a fair bit. There is a simpler description here.

The "CMA" part of "EUFCMA" implies that our adversary \(\mathbb{A}\), who we are now going to posit has the magical ability to forge signatures (so it's the black cube of our preamble), should be able to request signatures on an arbitrarily chosen set of messages \(m\), with \(i\) running from 1 to some defined number \(S\). But we must also allow him to make queries to the hash function, which we idealise as a machine called a "random oracle". Brief notes on that before continuing:

Aside: The Random Oracle Model

Briefly described here. It's a simple but powerful idea: we basically idealise how we want a cryptographic hash function \(f\) to behave. We imagine an output space for \(f\) of size \(C\). For any given input \(x\) from a predefined input space of one or more inputs, we will get a deterministic output \(y\), but it should be unpredictable, so we imagine that the function is randomly deterministic. Not a contradiction - the idea is only that there is no public law or structure that allows the prediction of the output without actually passing it through the function \(f\). The randomness should be uniform.

In using this in a security proof, we encounter only one problem: we will usually want to model \(f\) by drawing its output from a uniformly random distribution (you'll see lines like \(y \stackrel{\$}{\leftarrow} \mathbb{Z}_N\) in papers, indicating \(y\) is set randomly). But in doing this, we have set the value of the output for that input \(x\) permanently, so if we call \(f\) again on the same \(x\), whether by design or accident, we must again return the same "random" \(y\).

We also find sometimes that in the nature of the security game we are playing, one "wrapper" algorithm wants to "cheat" another, wrapped algorithm, by using some hidden logic to decide the "random" \(y\) at a particular \(x\). This can be fine, because to the "inner" algorithm it can look entirely random. In this case we sometimes say we are "patching the value of the RO at \(x\) to \(y\)" to indicate that this artificial event has occurred; as already mentioned, it's essential to remember this output and respond with it again, if a query at \(x\) is repeated.

Finally, this "perfectly random" behaviour is very idealised. Not all cryptographic protocols involving hash functions require this behaviour, but those that do are said to be "secure in the random oracle model (ROM)" or similar.

Wrapping A with B

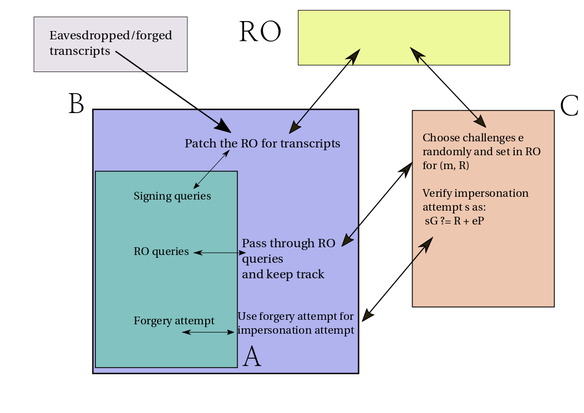
So we now wrap \(\mathbb{A}\) with \(\mathbb{B}\). And \(\mathbb{B}\)'s job will be to succeed at winning the SIDP "game" against a challenger \(\mathbb{C}\).

Now \(\mathbb{A}\) is allowed \(S\) signing queries; given his messages \(m_i\), we can use \(S\) eavesdropped conversations \(R, e, s\) from the actual signer (or equivalently, just forge transcripts - see "zero knowledgeness" of the Schnorr signature), and for each, \(\mathbb{B}\)can patch up the RO to make these transcripts fit \(\mathbb{A}\)'s requested messages; just do \(\mathbb{H}(m_i || R_i) = e_i\). Notice that this part of the process represents \(S\) queries to the random oracle.

Observe that \(\mathbb{B}\) is our real "attacker" here: he's the one trying to fool/attack \(\mathbb{C}\)'s identification algorithm; he's just using \(\mathbb{A}\) as a black box (or cube, as we say). We can say \(\mathbb{A}\) is a "subprotocol" used by \(\mathbb{B}\).

It's all getting a bit complicated, but by now you should probably have a vague intuition that this will work, although of course not reliably, and as a function of the probability of \(\mathbb{A}\) being able to forge signatures of course (we'll again call this \(\epsilon\)).

Toy version: \(\epsilon = 1\)

To aid understanding, imagine the simplest possible case, when \(\mathbb{A}\) works flawlessly. The key \(P\) is given to him and he chooses a random \(k\), \(R = kG\) and also chooses his message \(m\) as is his right in this scenario. The "CMA" part of EUF-CMA is irrelevant here, since \(\mathbb{A}\) can just forge immediately without signature queries:

• \(\mathbb{A}\) asks for the value of \(\mathbb{H}(m||R)\), by passing across \(m, R\) to \(\mathbb{B}\).
• \(\mathbb{B}\) receives this query and passes \(R\) as the first message in SIDP to \(\mathbb{C}\).
• \(\mathbb{C}\) responds with a completely random challenge value \(e\).
• \(\mathbb{B}\) "patches" the RO with \(e\) as the output for input \(m, R\), and returns \(e\) to \(\mathbb{A}\).
• \(\mathbb{A}\) takes \(e\) as \(\mathbb{H}(m||R)\), and provides a valid \(s\) as signature.
• \(\mathbb{B}\) passes through \(s\) to \(\mathbb{C}\), who verifies \(sG = R + eP\); identification passed.

You can see that nothing here is new except the random oracle patching, which is trivially non-problematic as we make only one RO query, so there can't be a conflict. The probability of successful impersonation is 1.

Note that this implies the probability of successfully breaking ECDLP is also
\(\simeq 1\). We just use a second-layer wrapper around \(\mathbb{B}\), and fork its execution after the provision of \(R\), providing two separate challenges and thus in each run getting two separate \(s\) values and solving for \(x\), the private key/discrete log as has already been explained.

Why \(\simeq\)? As noted on the SIDP to ECDLP reduction above, there is a tiny probability of a reused challenge value which must be factored out, but it's of course negligible in practice.

If we assert that the ECDLP is not trivially broken in reasonable time, we must also assert that such a powerful \(\mathbb{A}\) does not exist, given similarly limited time (well; in the random oracle model, of course...).

Full CMA case, \(\epsilon \ll 1\)

Now we give \(\mathbb{A}\) the opportunity to make \(S\) signing queries (as already mentioned, this is what we mean by an "adaptive chosen message attack"). The sequence of events will be a little longer than the previous subsection, but we must think it through to get a sense of the "tightness of the reduction" as already discussed.

The setup is largely as before: \(P\) is given. There will be \(h\) RO queries allowed (additional to the implicit ones in the signing queries).

• For any signing query from \(\mathbb{A}\) , as we covered in "Wrapping A with B", a valid response can be generated by patching the RO (or using real transcripts). We'll have to account for the possibility of a conflict between RO queries (addressed below), but it's a minor detail.
• Notice that as per the toy example previously, during \(\mathbb{A}\)'s forgery process, his only interaction with his wrapper \(\mathbb{B}\) is to request a hash value \(\mathbb{H}(m||R)\). So it's important to understand that, first because of the probabilistic nature of the forgery (\(\epsilon \ll 1\)), and second because \(\mathbb{A}\)'s algorithm is unknown, \(\mathbb{B}\) does not know which hash function query (and therefore which RO response) will correspond to a successful forgery. This isn't just important to the logic of the game; as we'll see, it's a critical limitation of the security result we arrive at.
• So to address the above, \(\mathbb{B}\) has to make a decision upfront: which query should I use as the basis of my impersonation attempt with \(\mathbb{C}\)? He chooses an index \(\omega \in 1 \ldots h\).
  There will be a total of \(S + h + 1\) queries to the random oracle, at most (the +1 is a technical detail I'll ignore here). We discussed in the first bullet point that if there is a repeated \(m, R\) pair in one of the \(S\) signing queries, it causes a "conflict" on the RO output. In the very most pessimistic scenario, the probability of this causing our algorithm to fail can be no more than \(\frac{S + h + 1}{n}\) for each individual signing query, and \(\frac{S(S+h+1)}{n}\) for all of them (as before we use \(n\) for the size of the output space of the hash function).
• So \(\mathbb{B}\) will fork \(\mathbb{A}\)'s execution, just as for the SIDP ECDLP reduction, at index \(\omega\), without knowing in advance whether \(\omega\) is indeed the index at the which the hash query corresponds to \(\mathbb{A}\)'s final output forgery. There's a \(\frac{1}{h}\) chance of this guess being correct. So the "partial success probability", if you will, for this first phase, is \(\frac{\epsilon}{h}\), rather than purely \(\epsilon\), as we had for the SIDP case.
• In order to extract \(x\), though, we need that the execution after the fork, with the new challenge value, at that same index \(\omega\), also outputs a valid forgery. What's the probability of both succeeding together? Intuitively it's of the order of \(\epsilon^2\) as for the SIDP case, but clearly the factor \(\frac{1}{h}\), based on accounting for the guessing of the index \(\omega\), complicates things, and it turns out that the statistical argument is rather subtle; you apply what has been called the Forking Lemma, described on Wikipedia and with the clearest statement and proof in this paper of Bellare-Neven '06. The formula for the success probability of \(\mathbb{B}\) turns out to be:

\(\epsilon_{\mathbb{B}} = \epsilon \left(\frac{\epsilon}{h} - \frac{1}{n}\right)\)

• Boneh-Shoup in Section 19.2 bundle this all together (with significantly more rigorous arguments!) into a formula taking account of the Forking Lemma, the accounting for collisions in the signing queries, to produce the more detailed statement, where \(\epsilon\) on the left here refers to the probability of success of \(\mathbb{B}\), and "DLAdv" on the right refers to the probability of success in solving the discrete log. The square root term of course corresponds to the "reduction" from Schnorr sig. to ECDLP being roughly a square:

\(\epsilon \le \frac{S(S+h+1)}{n} + \frac{h+1}{n} + \sqrt{(h+1) \times \mathrm{DLAdv}}\)

So in summary: we see that analysing the full CMA case in detail is pretty complicated, but by far the biggest take away should be: The security reduction for Schnorr sig to ECDLP has the same \(\epsilon^2\) dependency, but is nevertheless far less tight, because the success probability is also reduced by a factor \(\simeq h\) due to having to guess which RO query corresponds to the successful forgery.

(Minor clarification: basically ignoring the first two terms on the RHS of the preceding as "minor corrections", you can see that DLAdv is very roughly \(\frac{\epsilon^2}{h}\)).

The above bolded caveat is, arguably, very practically important, not just a matter of theory - because querying a hash function is something that it's very easy for an attacker to do. If the reduction loses \(h\) in tightness, and the attacker is allowed \(2^{60}\) hash function queries (note - they can be offline), then we (crudely!) need 60 bits more of security in our underlying cryptographic hardness problem (here ECDLP); at least, if we are basing our security model on the above argument.

Although I haven't studied it, the 2012 paper by Yannick Seurin makes an argument (as far as I understand) that we cannot do better than this, in the random oracle model, i.e. the factor of \(h\) cannot be removed from this security reduction by some better kind of argument.

Summary - is Schnorr secure?

For all that this technical discussion has exposed the non-trivial guts of this machine, it's still true that the argument provides some pretty nice guarantees. We can say something like "Schnorr is secure if:"

• The hash function behaves to all intents and purposes like an ideal random oracle as discussed
• The ECDLP on our chosen curve (secp256k1 in Bitcoin) is hard to the extent we reasonably expect, given the size of the curve and any other features it has (in secp256k1, we hope, no features at all!)

This naturally raises the question "well, but how hard is the Elliptic Curve discrete logarithm problem, on secp256k1?" Nobody really knows; there are known, standard ways of attacking it, which are better than brute force unintelligent search, but their "advantage" is a roughly known quantity (see e.g. Pollard's rho). What there isn't, is some kind of proof "we know that \(\nexists\) algorithm solving ECDLP on (insert curve) faster than \(X\)".

Not only don't we know this, but it's even rather difficult to make statements about analogies. I recently raised the point on #bitcoin-wizards (freenode) that I thought there must be a relationship between problems like RSA/factoring and discrete log finding on prime order curves, prompting a couple of interesting responses, agreeing that indirect evidence points to the two hardness problems being to some extent or other connected. Madars Virza kindly pointed out a document that details some ideas about the connection (obviously this is some pretty highbrow mathematics, but some may be interested to investigate further).

What about ECDSA?

ECDSA (and more specifically, DSA) were inspired by Schnorr, but have design decisions embedded in them that make them very different when it comes to security analysis. ECDSA looks like this:

\(s = k^{-1}\left(\mathbb{H}(m) + rx\right), \quad r= R.x, R = kG\)

The first problem with trying to analyse this is that it doesn't conform to the three-move-sigma-protocol-identification-scheme-converts-to-signature-scheme-via-Fiat-Shamir-transform. Why? Because the hash value is \(\mathbb{H}(m)\) and doesn't include the commitment to the nonce, \(R\). This means that the standard "attack" on Schnorr, via rewinding and resetting the random oracle doesn't work. This doesn't of course mean, that it's insecure - there's another kind of "fixing" of the nonce, in the setting of \(R.x\). This latter "conversion function" is kind of a random function, but really not much like a hash function; it's trivially "semi-invertible" in as much as given an output x-coordinate one can easily extract the two possible input R-values.

Some serious analysis has been done on this, for the obvious reason that (EC)DSA is very widely used in practice. There is work by Vaudenay and Brown (actually a few papers but I think most behind academic paywalls) and most recently Fersch et al. Fersch gave a talk on this work here .

The general consensus seems to be "it's very likely secure - but attempting to get a remotely "clean" security reduction is very difficult compared to Schnorr".

But wait; before we trail off with an inaudible mumble of "well, not really sure..." - there's a crucial logical implication you may not have noticed. Very obviously, ECDSA is not secure if ECDLP is not secure (because you just get the private key; game over for any signature scheme). Meanwhile, in the long argument above we reduced Schnorr to ECDLP. This means:

If ECDSA is secure, Schnorr is secure, but we have no security reduction to indicate the contrary.

The aforementioned Koblitz paper tells an interesting historical anecdote about all this, when the new DSA proposal was first put forth in '92 (emphasis mine):

"At the time, the proposed standard — which soon after became the first digital signature algorithm ever approved by the industrial standards bodies — encountered stiff opposition, especially from advocates of RSA signatures and from people who mistrusted the NSA's motives. Some of the leading cryptographers of the day tried hard to find weaknesses in the NIST proposal. A summary of the most important objections and the responses to them was published in the Crypto'92 proceedings[17]. The opposition was unable to find any significant defects in the system. In retrospect, it is amazing that none of the DSA opponents noticed that when the Schnorr signature was modified, the equivalence with discrete logarithms was lost."

More exotic constructions

In a future blog post, I hope to extend this discussion to other constructions, which are based on Schnorr in some way or other, in particular:

• The AOS ring signature
• The Fujisaki-Suzuki, and the cryptonote ringsig
• the Liu-Wei-Wong, and the Monero MLSAG (via Adam Back) ringsig
• The MuSig multisignature

While these are all quite complicated (to say the least!), so no guarantee of covering all that, the security arguments follow similar lines to the discussion in this post. Of course ring signatures have their own unique features and foibles, so I will hopefully cover that a bit, as well as the security question.